When teaching quadratic sequences, particularly finding the position to (nth) term rule, I find that the students are fairly quick at understanding where each part of the rule comes from when the sequence is in the form an^2, n^2 + c and an^2 + c. This is especially true if they're shown a very basic general quadratic sequence which shows the second difference to always be twice the coefficient of n^2.
The difficulty for students occurs when the quadratics have a rule that is in the form an^2 +bn +c. It is quite difficult for them to understand that the quadratic sequence can be built up by combining one of the previosuly mentioned sequences with a linear sequence too.
To aid the students, I made this task which aimed to show them visually what was happening when we moved from term to term. We looked through the first 4 examples together, each example appearing separately so we could focus on how the terms were being formed each time.
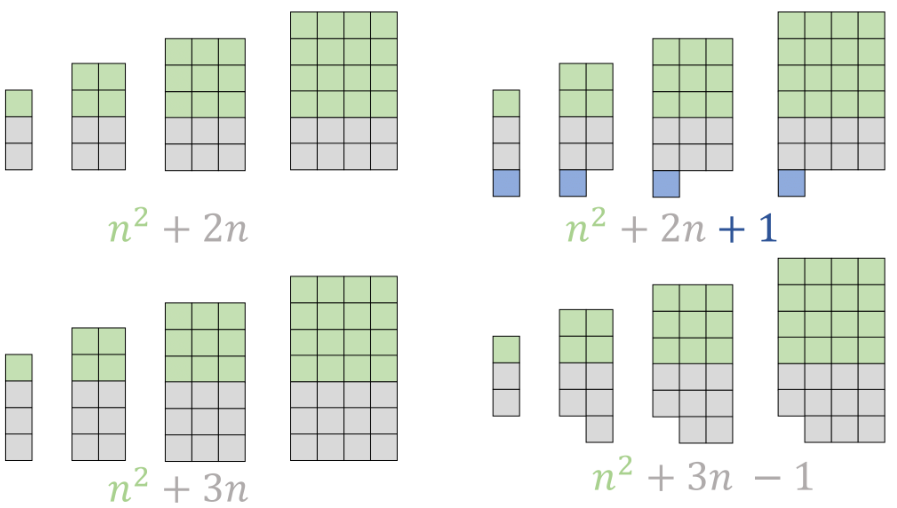
The students then worked independently for a short while on this matching activity before sharing their solutions with their partners. The matching activity included 7 visual sequences, 7 rules and 2 blank boxes. The blank boxes did not match up together so for the last couple of sequences the students had to draw a diagram based on the nth term rule and also find the nth term rule for the sequence represented by the final diagram.
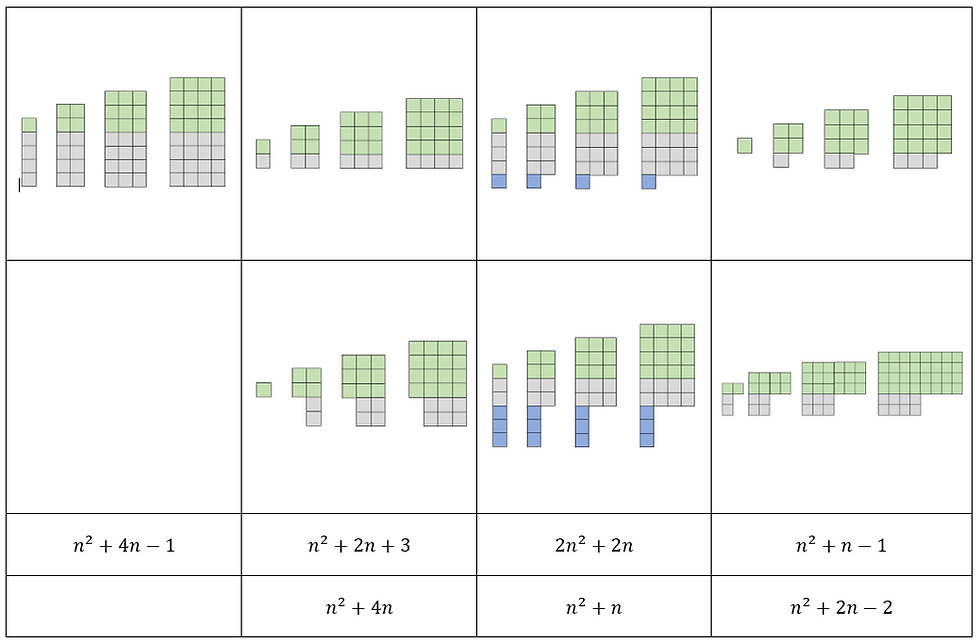
The students were quickly able to recognise the different parts of the nth term rule and how each part helped to build the term. This meant that during the following lesson when we began to find the nth term of quadratic sequences without diagrams the students were unfazed by the prospect of combining a linear sequence with a quadratic sequence to get to the sequence they had been given.
Find a downloadable version of the matching activity in the link: https://drive.google.com/file/d/1dZj1k0hxoFS_xiWvZ-8TvCeihjjUoh6Z/view?usp=sharing
Comentarios