When working with circles and sectors I remember that I used to begin to write things down before I'd fully read the question. Information that I knew just from looking at the diagram that could prove useful. As with goal free problems in general I think its a useful skill for a student to look at a diagram and be able to write things down about the diagram that they knew from either inspection or minimal working out. In this case - the radius length, the diameter length and the fraction of a full circle on display.
This is where my idea - based on a layout I'd seen from Chris McGrane on startingpointsmaths - began to take shape. I decided that with the perimeter of a sector the key ideas were to be able to understand how much of the whole circle was there, what the length of the arc was, what the length of the straight lengths had to be and to be able to communicate this with and without a calculator (in terms of pi and to one decimal place).
You can see we started with some straight forward questions - standard to those you would expect to meet in the early stages of this concept. I followed on from this with a couple of questions that tested whether the students understood exactly where the numbers were coming from in the 2nd, 3rd and 4th columns.
Once students had completed these the introduction of sectors (see corbettmaths for more excellent banks of questions such as the sector diagrams you see below).
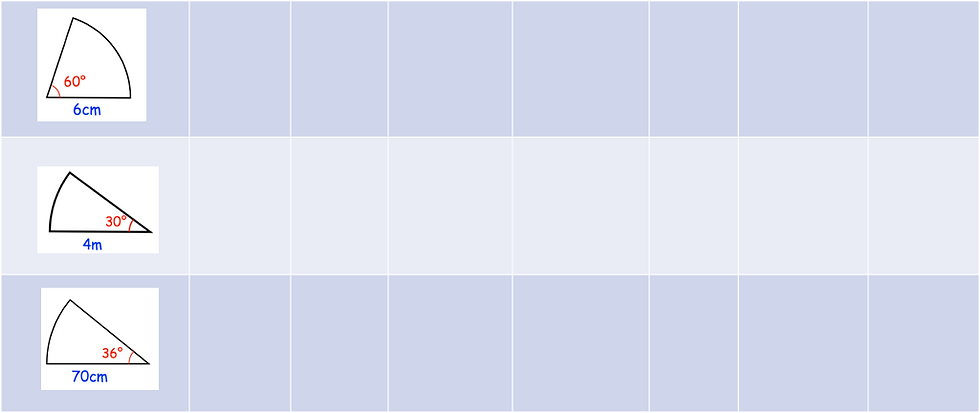
We finished off sectors with some similar to those seen previously where the diagram is absent from the question. Before finally ending with questions that require the student to go completely backwards from the answer.
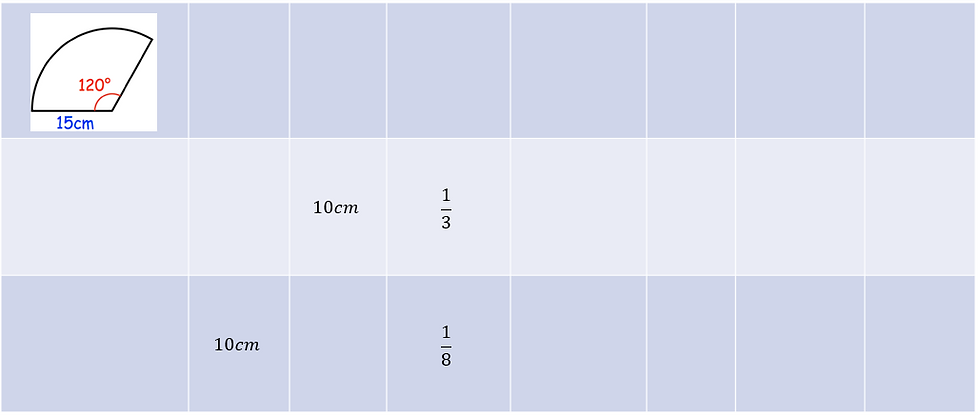
A common theme in my tasks I have been putting together recently has been the opportunity for students to work both forwards and backwards and believe this is making my students more flexible when approaching unfamiliar problems.
For the downloadable version of the task follow the link: