I've found that this is an idea in Maths that can often be treated as a bolt on.
With this in mind I wanted to create some questions that allowed students to practice recognising and labelling horizontal and vertical lines that reinforces the idea that these equations simply describe the relationship between a set of points - in this case - a common characteristic.
We start off with some really standard questions, if they can't decide on the equations of these lines then I've done something wrong in the lead up to this task.
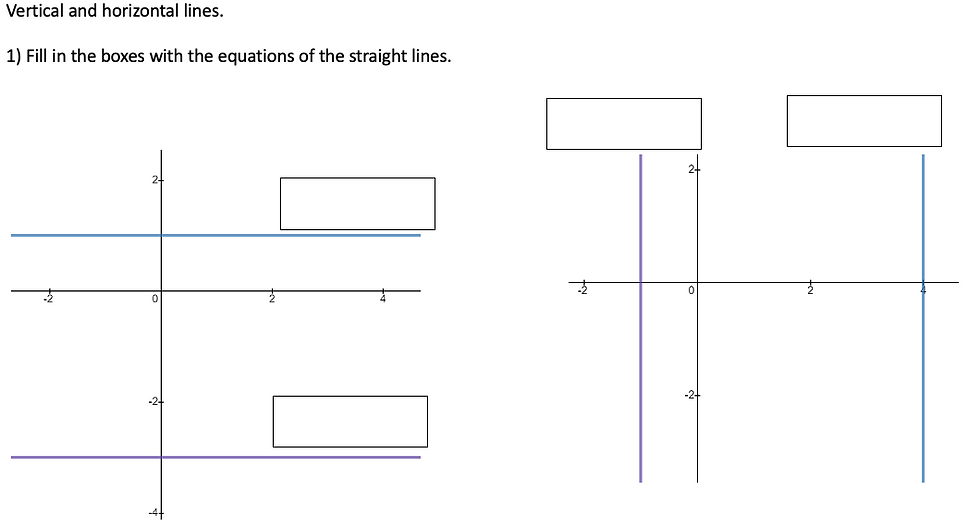
Question 2 and 3 build on the idea that we don't have to memorise which equations represent horizontal and which represent vertical lines. I want them to focus on the common characteristic between the points given.
Question 4 drives home the idea that any point will always have 1 unique horizontal and 1 unique vertical line that passes through it. We may talk about there being an infinite number of diagonal lines that would intersect a point if it comes up in the discussion.
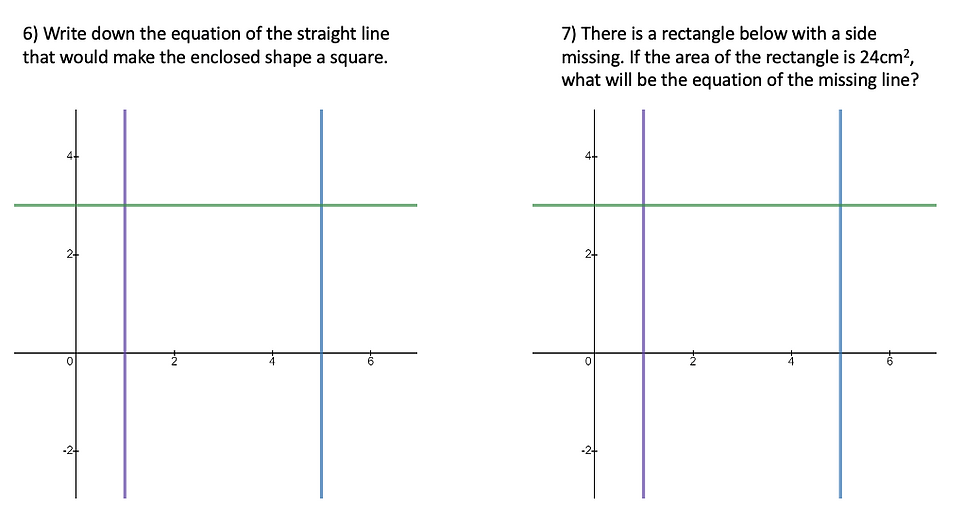
Questions 5, 6 and 7 then provide the students an opportunity to apply this knowledge and understanding to a new context. I wanted to interleave to ensure that whilst we over practiced with equations of V and H lines the students had a purpose for this practice.
Find the complete lesson linked here: https://drive.google.com/file/d/1Ti0J3uOXQBh9j2H-bSxA1n-3HPtiCjCR/view?usp=sharing